

This effectively exchanges the X and Y coordinates for each point on the graph: x' = y, y' = x. Next you flip the sheet over a second time by holding the bottom-left and top-right corners, such that they remain where they are but the top-left and bottom-right corners exchange positions. The new graph is effectively x' = -x, y' = y. The vertical coordinates for all points on the graph remain unchanged. You begin by flipping the sheet over horizontally: everything on the left side of the graph moves to the right and everything on the right moves to the left. You manipulate the orientation of the sheet in order to transform the graph. There is a graph of some sort plotted on it as well. Write P as a vector sum.Imagine you have some coordinate axes printed on a square transparent sheet. Since we now know what P1' and P2' are, we can find P' as the missing vertex of the rectangle. In more geometrical words, the rectangle OP1PP2 is rotated to a rectangle OP1'P'P2'. The point P' can be obtained by taking a vector sum.What is h in this case when P = (a,b) and what are the coordinates of P2'? Since P2' is on line OE2', then P2' is a multiple of E2'.Hint: What is OP1'/OE1'? It is equal to OP1/OE1. What is k in this case when P = (a,b) and what are the coordinates of P1'? Since P1' is on line OE1', then P1' is a multiple of E1'.What did you learn about rotation by 90 degrees? Note that distance ratios are the same after rotation. We denote the rotated points by adding a prime (e.g., the rotation of E1 is E1'). Now suppose that this entire figure is rotated by angle u, with center of rotation = O.
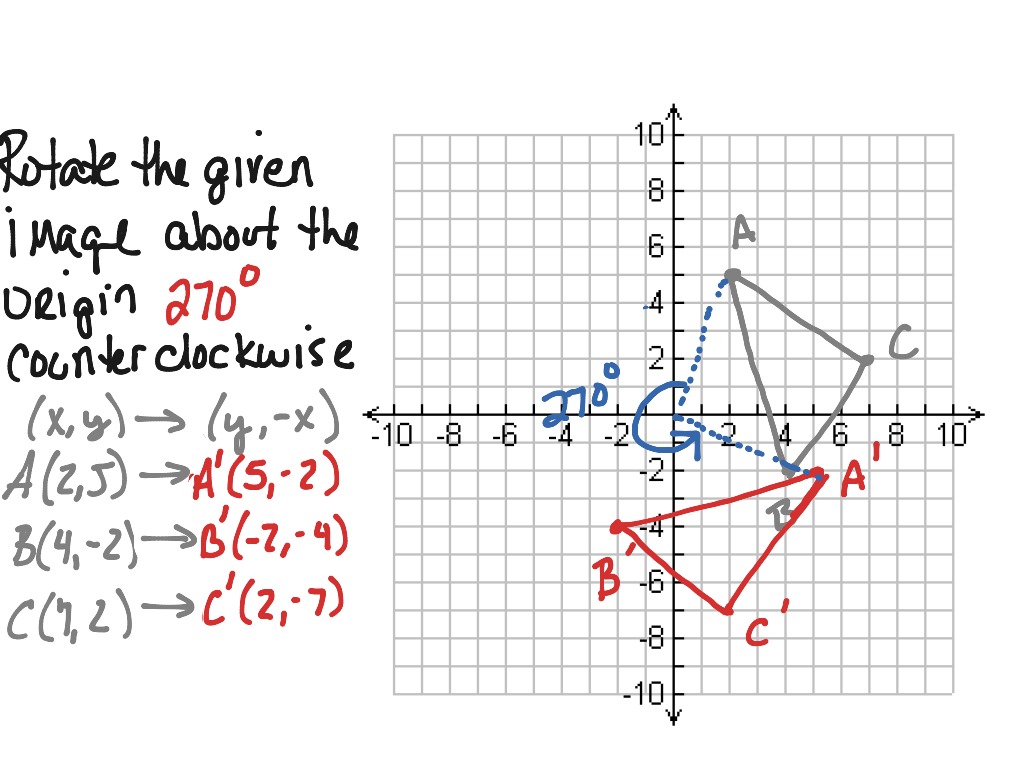
The x-axis is the line OE1 and the y-axis is the line OE2. If P = (1,-2), find the coordinates of all the labeled points in the figure. We denote the rotated points by adding a prime (e.g., the rotation of E1 is E1', etc.). The entire figure is rotated by angle u, with center of rotation = O, so that the x-axis OE1 is rotated to a line through X = (-2,2). Suppose that on the plane, O, E1, and E2 and points P, P1, and P2 be as in Example 1, with coordinate axes OE1 and OE2. Given that the x-axis is rotated to the line OX, with X = (4,3), if P = (3.2), find the coordinates of all the labeled points in the figure We denote the rotated points by adding a prime (e.g., the rotation of E1 is E1', etc.) Now suppose that this entire figure is rotated by angle u, with center of rotation = O. These figures may help you figure out or explain the formula. Check that this works even if Q is not in the first quadrant, for example, if Q1=(-3,2), what is Q1'?.If Q' is obtained by rotating Q by 90 degrees with center O = (0,0), what are the coordinates of Q? Then P' is obtained by rotating P by 90 degrees with center O = (0,0). Draw on graph paper the point P with coordinates (3,4).When points A, B, C are on a line, the ratio AC/AB is taken to be a signed ratio, which is negative is A is between B and C.įormula for rotation of a point by 90 degrees (counter-clockwise) They may help you put the whole picture together.
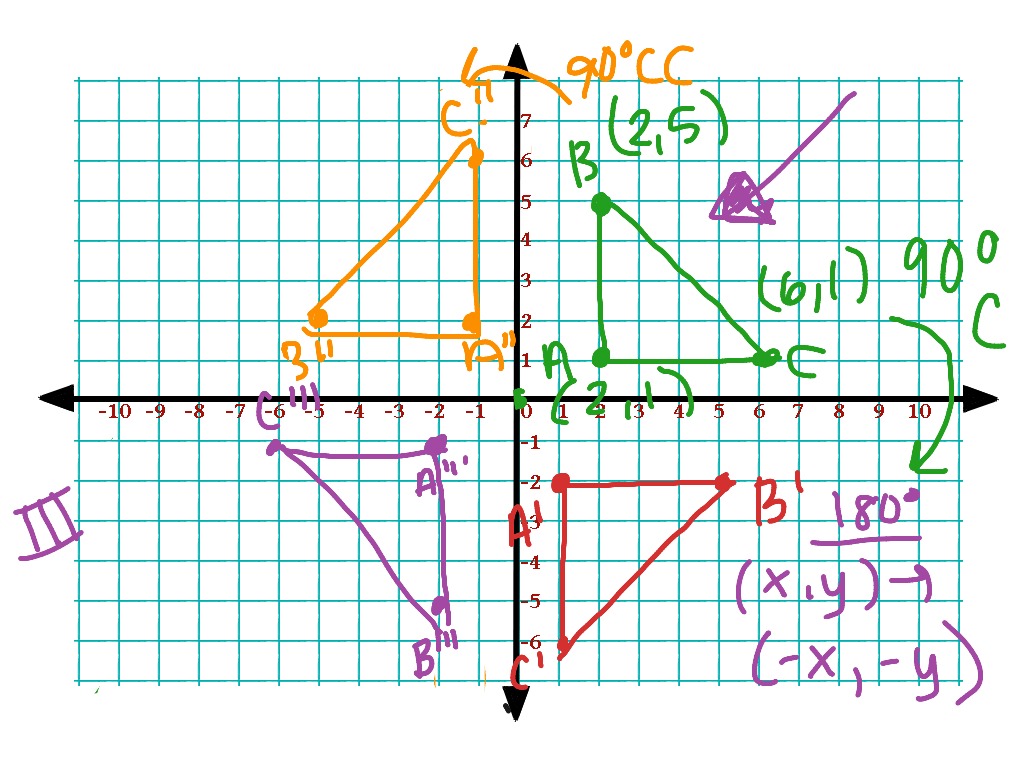
Here is a set of practice exercises to work and some explanations for you to contemplate. There are a number of ingredients that go into the general formula for rotation in the (x,y) plane.


 0 kommentar(er)
0 kommentar(er)
